Audio音频入门
在反复纠结两个月后,本人最后还是选择之后整音频方向,以后会将自己学音频相关的笔记放到博客上,先学习音频分类吧。
最后吐槽一下:密码学真的是Bar又高又吃不饱饭,虽然有20和21年很多大厂在政策影响下招了隐私计算岗,但这几年已经不会再招多少人了(几乎只有蚂蚁和华为有位置),区块链厂更不说了主打的就是不稳定。
1. 音频基本介绍
音频一般指人耳可以听到的频率在20Hz-20kHz之间的声波,也可以指像.WAV这样存储音频信息的文件。它有如下三要素:
- 振幅:声波振动大小,也就是响度
- 频率:声波振动的频率,可以理解为音调
- 波形:决定声波的形状,可以决定声音的音色
1.1. 音频数据的存储方式
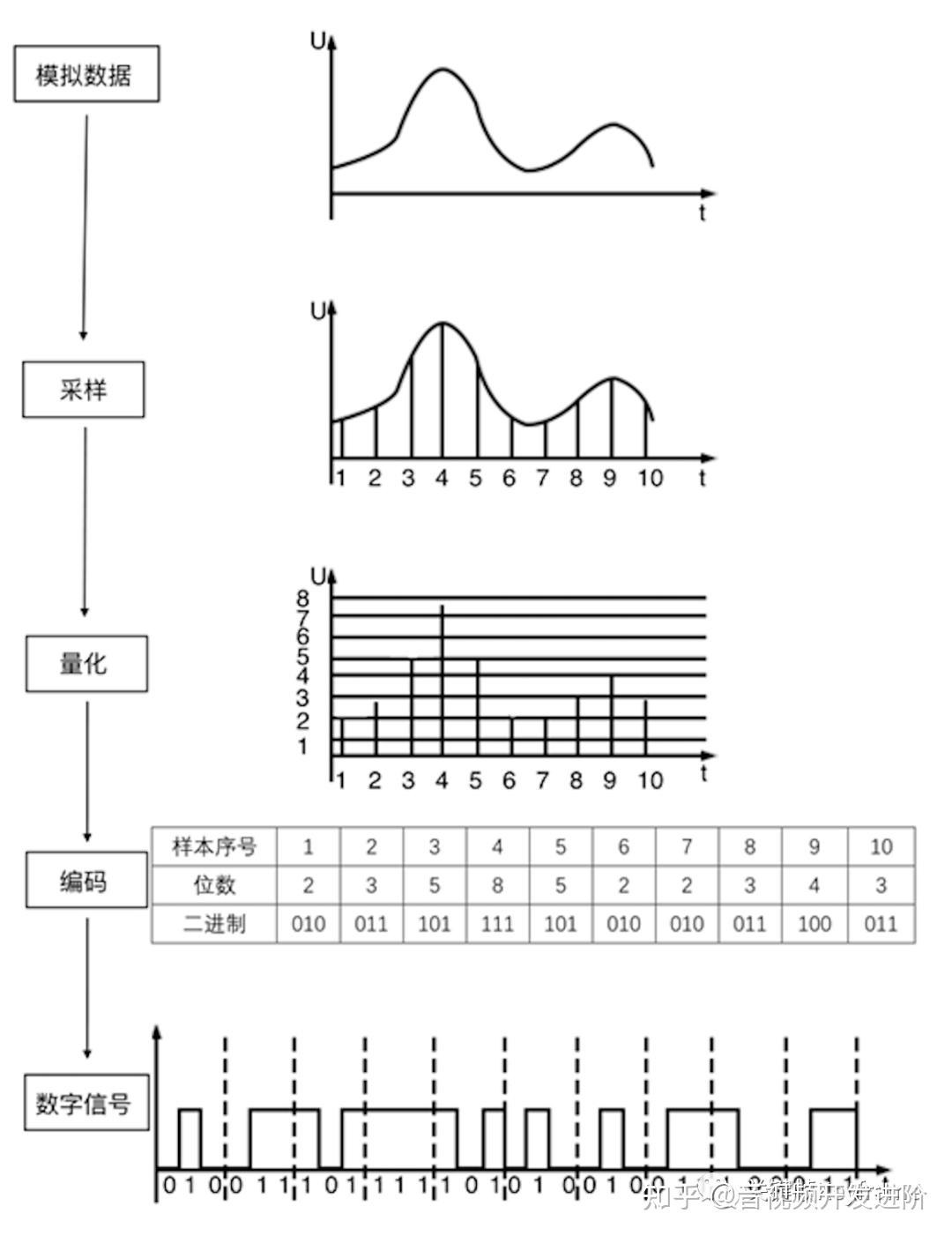
一般来说,使用脉冲编码调制(PCM)来编码音频,它对连续变化的模拟信号进行抽样、量化和编码产生数字信号。
- 抽样:将连续时间模拟信号变为离散时间、连续幅度的抽样信号
- 量化:将抽样信号变为离散时间、离散幅度的数字信号
- 编码:对每组数据的幅度进行编码
此外还有几个相关概念:
- 采样率:记录声音时每秒的采样个数,它用赫兹(Hz)来表示。
- 量化格式(采样深度):指记录声音的动态范围,它以位(Bit)为单位。
- 声道数:通道的数目
- 比特率:每秒传输的数据量,比特率/码率 = 采样率 × 采样深度 × 通道数。kbps
- 音频编码:仅仅由0和1构成的编码表示不同的振幅
- 声道数:每次生成一个声波数据成为单声道,每次生成两个声波数据称为双声道
- 音频率:比特率/8
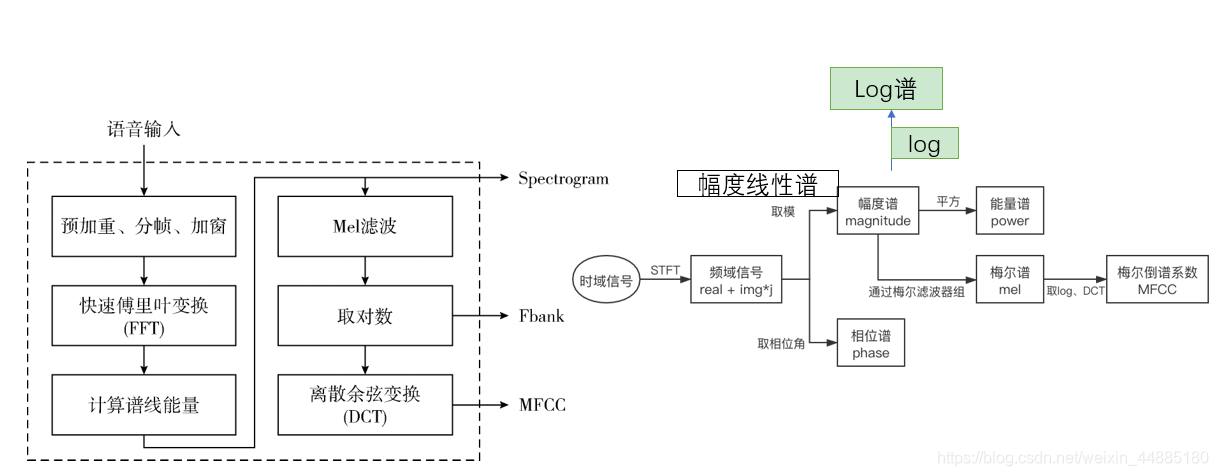
1.2. 语谱图、Fbank、MFCC之间的关系
一般来说,将音频数据输入到神经网络中需要将其预处理为语谱图(log谱)、Fbank或者MFCC,目前为了让神经网络接收到的信息足够多,一般还需要将音频的相位谱也作为输入传输到神经网络中,此时神经网络的输入大小为$B\times 2\times W\times T$,$B$为batch,2为语谱图/Fbank/MFCC和相位谱,$W$为频率范围,$T$为时间。
2. 从音频到语谱图
预加重、预增强
预增强以帧单位进行,目的在于加强高频,增加语音的高频分辨率。预加重后的结果为
$k$是与增强系数,范围$[0,1)$,常用0.97,$x$是提取的wav时域数组的项
分帧
分帧是将不定长的音频切分成固定长度的小段,现实中大多数信号都是非平稳的,但大多数短时间内可以近似看做是平稳的,可以用短时傅里叶变换表现非平稳信号频域特征。 需要分帧是因为后续的傅里叶变换适用于分析平稳的信号,而语音信号是变化迅速的 。
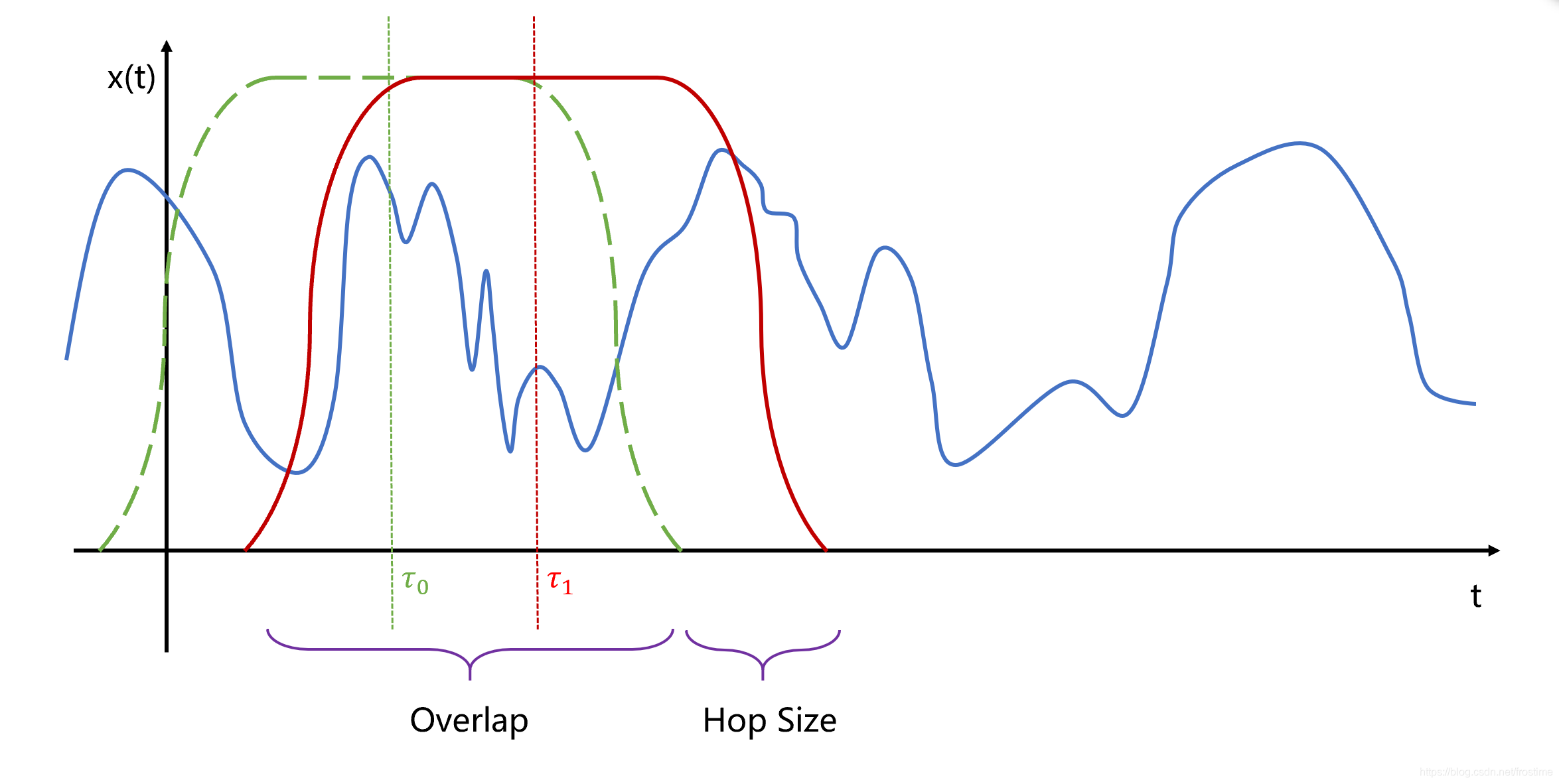
为了避免窗边界对信号的遗漏,因此对帧做偏移时候,帧间要有重叠一部分。通常的选择是帧长25ms,帧移为10ms。接下来的操作是对单帧进行的。要分帧是因为语音信号是快速变化的,而傅里叶变换适用于分析平稳的信号。帧和帧之间的时间差常常取为10ms,这样帧与帧之间会有重叠,否则,由于帧与帧连接处的信号会因为加窗而被弱化,这部分的信息就丢失了。

加窗
傅里叶变换要求输入信号是平稳的,但是语音信号从整体上来讲是不平稳的。每帧信号通常要与一个平滑的窗函数相乘,让帧两端平滑地衰减到零,这样可以降低傅里叶变换后旁瓣的强度,取得更高质量的频谱。
分帧截断时域信号的两旁会出现旁瓣,导致频谱泄露。因为声音信号是非周期信号,截取任意有限长的序列都不能代表原信号,矩形窗的频域是Sa函数,旁瓣起伏大,会产生频谱失真。所以一般采用汉明窗,它具有较小的旁瓣。以下是一个窗函数的示例
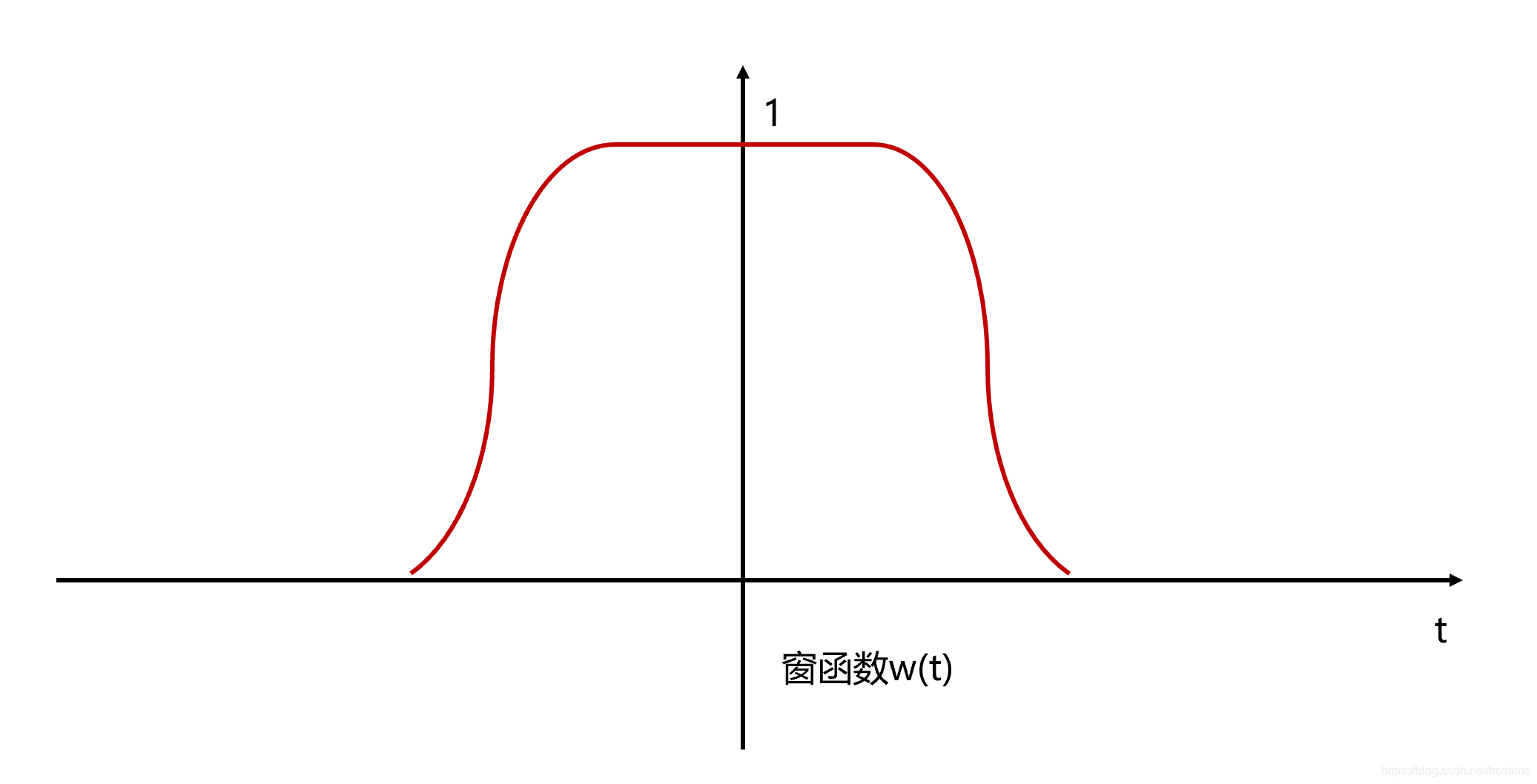
将窗函数和原始信号相乘就可以获得截取后的信号 $y(t)$。
$$
y(t)=x(t)\cdot w(t-\tau)
$$
之后对分帧后的每个帧都用这样的窗函数处理,就可以将每帧两侧的旁瓣减弱,经过傅里叶变换后,可以获得更高质量的频谱。
快速傅里叶变换
即使是分帧过后极短时间的声音,仍是很多高低频声音的混杂,此时的数据是时域,通过傅里叶变换转换为频域可以将复杂声波分成各种频率的声波,方便神经网络进行学习。最终结果是个频率范围内的重要程度(能量)。
因为我们用的是数字音频,所以我们用到的是离散傅里叶变换。我们现在可以在每一帧上做N点FFT来计算频谱,也称为短时傅里叶变换(Short-Time Fourier-Transform, STFT),其中N通常为256或512,NFFT = 512。公式如下所示,其中$x_i$为信号$x$的第$i$帧:
$$
P=\frac{|FFT(x_i)|^2}{N}
$$
将得到的每一帧的变换按轴频率轴拼接在一起就成了语谱图。纵轴表示频率,横轴表示时间,颜色的深浅来代替频谱强度。

3. 从语谱图到Fbank
人耳对声音频谱的响应是非线性的,如果我们能类似于人耳的方式对音频进行处理,可以提高语音识别的性能。耳蜗的滤波作用是在对数频率尺度上进行的,在1000HZ以下为线性尺度,1K HZ以上为对数尺度,使得人耳对低频信号敏感,高频信号不敏感。FilterBank就是这样的一种算法。FBank特征提取要在预处理之后进行,这时语音已经分帧,我们需要逐帧提取FBank特征。生成Fbank需要对频谱图进行对Mel滤波和对数运算。
Mel滤波器组
梅尔标度被提出,它是频率Hz的非线性变换,对于以mel scale为单位的信号,可以做到人们对于相同频率差别的信号的感知能力几乎相同。梅尔频率与实际频率的关系为:Hz ($f$) 和 Mel ($m$),$m=F_{mel}(f)=2595\cdot log_{10}(1+\frac{f}{700}), f=F^{-1}_{mel}(m)=700(10^{m/2595}-1)$
计算fbank的最后一步是在得到的功率谱上应用三角形滤波器,通常是40个滤波器。滤波器如下所示:
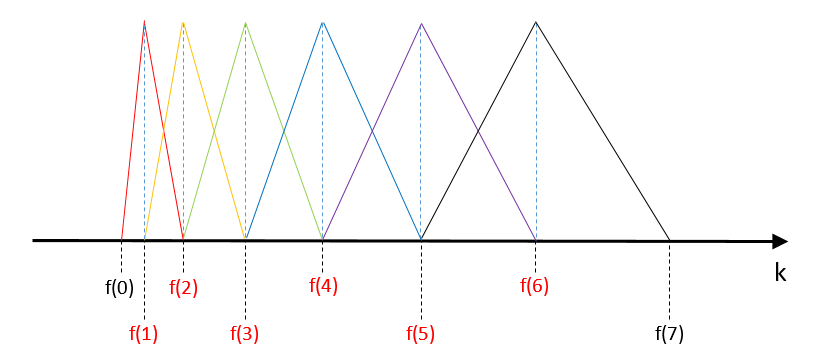
- 当声波频率小于$f(0)$或大于$f(6)$时,滤波器组的和等于0,该声波会被完全过滤掉
确定这些$f(1)~f(6)$需要以最低频率$f_l$,最高频率$f_h$,傅里叶变换时的长度$N$,音频采样率$f_s$,对于第$m$个点$f(m)$计算如下:
$$
f(m)=(\frac{N}{f_s})F^{-1}{mel}(F{mel}(f_l)+m\frac{F_{mel}(f_h)-F_{mel}(f_l)}{M+1})
$$
将Mel滤波器组应用于信号的语谱图(也就是语谱图的矩阵和Mel滤波器的矩阵相乘),然后过滤后的语谱图取$log_{10}$再乘20,得到fbank,fbank的纵坐标表示在某个帧内,不同的滤波器的过滤后并取对数的结果:$s(m)=20*log(f(m))$
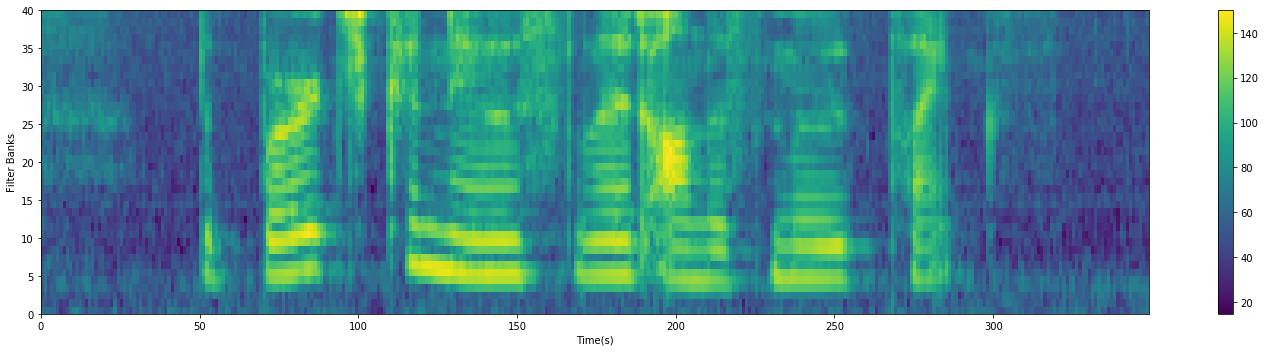
代码如下:
1 | def mel_filter(frame_pow, fs, n_filter, nfft): |
4. 从Fbank到MFCC
事实证明,前一步计算出的滤波器组系数高度相关,这在某些机器学习算法中可能存在问题。因此,我们可以应用离散余弦变换(DCT)去相关滤波器组系数并产生滤波器组的压缩表示(用cos函数的值作为系数,求对每个滤波器的取对数输出的加权和),其中$L$是MFCC系数阶数,一般取12-16。
$$
C(n)=\sum^{M-1}_{m=0}s(m)cos(\frac{\pi n(m-0.5)}{M}),n=1,2,…,L
$$